Особенности при работе с тестовыми заданиями в системе дистанционного обучения. ☼

Автор: Питц Татьяна Александровна

На сегодняшний день, при реализации тестирования в системах дистанционного обучения, используются следующие формы вопросов (заданий) [1]:

1-я форма — задание с выбором правильного ответа (одного из множества или нескольких из множества) или закрытая форма.

2-я - открытая форма, где студент сам вписывает (набирает с клавиатуры) ответ в отведенное место (“задание на дополнения” или “задание с конструируемым ответом”).

3-я форма тестового задания - задание на установление соответствия, где элементам одного множества требуется поставить в соответствие элементы другого множества.

В 4-ой форме требуется установить правильную последовательность хаотично представленных объектов.

Среди этих форм заданий, задания первой формы, на сегодняшний день, во всех системах дистанционного обучения занимают 80% – 90%, остальные формы занимают только 10%-20% в связи с тем, что их трудно реализовать.

Использование выборочных ответов сопряжено с возможностью неадекватной оценки знаний обучаемого в случае случайного ввода правильного ответа [2]. Оценим эту вероятность для предложения верного подхода.

1.                  Для заданий открытой формы, вероятность случайного ввода правильного ответа практически равна нулю. Это похоже на случай, когда вы должны искать пароль чужого человека и не знаете, какая длина у этого пароля.

2.                  Для вопросов типа: "N вариантов ответов – из них один правильный". Эта вероятность равна:  

3.                  Для вопросов типа: "N вариантов ответов – из них k правильных" (0 ≤ k ≤ N) вероятность ввода каждого ответа для выборки длиной kне зависит от числа правильных вариантов, так как студент может выбрать от 0 до N вариантов, то все возможные комбинаций ответов составляют вариантов. А верный вариант только один, поэтому вероятность того, чтобы студент выбрал верный ответ, равна: 

4.                  Для вопросов типа установления правильной последовательности хаотично представленных N объектов количество возможных вариантов – это число перестановок из N элементов и равно N!. Отсюда вероятность случайного выбора правильного ответа равна 

5.                  Для вопросов типа установления соответствия, где k элементам одного множества требуется поставить в соответствие N элементов другого множества. При этом каждый элемент в обоих множествах не повторяется. То есть один элемент первого множества соответствует только одному элементу другого множества.  Количество различных вариантов равно числу размещений из N элементов по k без повторений и равно . Отсюда вероятность случайного выбора правильного ответа равна: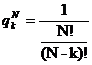

a.                   На практике не редко встречаются вопросы типа установления соответствия, где k элементам одного множества требуется поставить в соответствие N элементов другого множества. При этом элемент в правом столбце может появляться несколько раз. В этом случае  количество различных вариантов равно числу размещений из N элементов по k с повторением и равно . Отсюда вероятность случайного выбора правильного ответа равна: 

Изменение вероятности случайного ввода правильного ответа в зависимости от количества вариантов для разных схем показано в нижней таблице.

Из верхней таблицы можем сделать следующие выводы:

·                    Вопрос типа N вариантов – k верный лучше, чем ответ типа N вариантов – 1 верный, так как при одинаковом количестве вариантов вероятность случайного выбора верного ответа при типе N вариантов – k верный меньше.

·                    При увеличении чисел вариантов результат тестирования тоже улучшается, так как при этом вероятность уменьшается.

·                    Для вопросов типа установления соответствия при увеличении значения К вероятность случайного выбора верного ответа уменьшается.

Рекомендации при реализации тестирования.

Из данного анализа мы можем сформулировать следующие рекомендации:

Оптимальное число элементов ответа (альтернатив): с выбором “одного из множества” – 1-го из 2-8, оптимально 1 из 6; “несколько из множества” – 2-10 из 6-12; на соответствие – 3-6 левый столбец, на 1-2-3, до в 2 раза больше элементов — правый; на последовательность – 3-9

С целью нивелирования заимствования ответа у соседа надо формулировать тестовые задания в 2-3-х синонимичных по смыслу вариантах, которые выбираются случайным образом. Элементы задания в этих формах формируются по принципу “основных” и “запасных” игроков. Например, при пяти элементах, подающихся студенту, автор формирует набор не “1 верный + 4 неверных, а “1 верный + 4 основных неверных + 5 запасных неверных”, где из 9-ти случайным образом выбираются четыре.

При вопросах типа установления соответствия:

·                     элементы задающего столбца располагаются слева, а элементы выбора - справа;

·                     в правом столбце формируется, например, на 1-3 элемента, но не более чем в 2 раза больше элементов, чем в левом, чтобы при последней подстановке у студента был выбор, а не автоматически подставляемый остаток.

Литература.

1.                  Аванесов В. С. Форма тестовых заданий. Учебное пособие для учителей школ, лицеев, преподавателей вузов и колледжей. 2 изд., переработанное и расширенное. - М.: Центр тестирования, 2005. - С. 17.

2.                  Карпова И. П. Исследование и разработка подсистемы контроля знаний в распределительных автоматизированных обучающих системах./ Москва 2002.